
未等式というのはあまり聞きなれないかもしれませんが、上記のような問題を「未等式」と呼びます。
パズルのように見えますが、解き方を知らずに解こうとすると骨が折れます。上記のように数が小さく、項も少ない場合は総当たりでも高々23=8通りしかありませんが、項が増えると文字通り指数関数として場合が増えますので大変です。
確実に解ける方法がありますので以下に書いておきます。プリントを解くときにもこの解き方でやるようにご指導するのが良いかと思います。小学校低学年で初見だと、ほぼ思いつかないと思います。
上の問題を例にします。

まず、左辺の数をすべて足します。
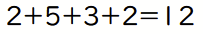
これから、右辺、つまり6を引きます。
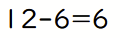
これの半分に相当する分だけ「-」とすると答えになります。
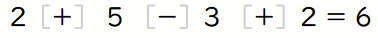
理屈としては、全部足した場合は、本来「引く」数字を引かないだけでなく、さらに「足す」ことになるため、全部足したものと式の右辺の差は、「引く数字」の2倍となります。
初版/最新版 2023-09-22/2023-09-22